平方根の身近な例

平方根の身近な例
こんなところで使うの?身近な平方根の世界 🎓🔢✨
こんにちは。みなさんは数学の授業で 平方根(へいほうこん) を習っていると思います。平方根というと、「√(ルート)」の記号が出てきて、少し難しそうに感じるかもしれません。日常とはかけ離れているように思えますね。
平方根って身近に例はあるんでしょうか?
実は平方根は日常生活のさまざまな場面で使われています。今日は、平方根の身近な例として、生活の中で平方根がどんなところで役立っているのかを紹介します。📘📐🖊️
その1:テレビやスマホの画面サイズ 📺📏📱
テレビやスマホを買うとき、「50インチ」や「6.7インチ」といった画面のサイズをよく耳にします。この「インチ」というのは、実は画面の 対角線の長さ を表しています。
例えば、縦が90cm、横が160cmのテレビがあったとします。このとき、対角線の長さは 三平方の定理 を使って計算します。
縦² + 横² = 対角線²
90² + 160² = 対角線²
→ 8100 + 25600 = 33700
→ 対角線² = 33700
したがって、対角線の長さは √33700。計算すると約183.5cm です。つまり、このテレビは約72インチほどの大きさだと分かります。こうした計算は、テレビを設置するスペースを決めるときや、スマホの画面サイズを比較するときに役立ちます。📊🛠️🖥️
平方根の身近な例の最も良い例ですね。
その2:地震の揺れの強さを知る 🌏📈🏢
日本は地震が多い国で、ニュースなどで「震度○」や「マグニチュード○」という言葉を耳にすることがあります。震度や揺れの強さを考えるとき、加速度 という値が重要です。加速度は、地面がどれだけ速く動くかを表します。
建物の耐震設計などでは、この加速度の計算に平方根が使われます。例えば、建物がどれくらい揺れやすいかを示す 固有周期(一回揺れるのにかかる時間)は、建物の高さ H にほぼ比例し、
T = C × √H
という式で表されることがあります。(C は建物の構造などによって決まる定数です。)
このように、揺れの分析や安全設計の場面でも平方根が大切な役割を果たしています。📝🧩🛠️
その3:デザインやアートの世界でも 🎨📐🖼️
「黄金比」という言葉を聞いたことがある人もいるでしょう。これは、古代から美術や建築で「美しい」とされてきた比率です。
黄金比は、
(1 + √5) ÷ 2 ≈ 1.618…
という式で表されます。このように、黄金比には平方根が含まれています。
例えば、
- 美術作品の構図
- 写真のトリミング
- 建物の設計
など、さまざまな場面で黄金比が使われます。黄金比を取り入れると、見た目が整い、美しく感じられることが多いです。普段目にするポスターやウェブサイトのデザインにも、こうした数学の知識が活かされていることがあります。✨🖌️🏛️
その他の平方根が活躍する場面 ✨🔍📏
ここまで紹介したもの以外にも、平方根は生活のさまざまな場面で使われています。いくつか例を挙げます。📖💡🛠️
📐 正方形の面積から一辺を求めたいとき
例えば、部屋に 正方形のマット を敷きたいとします。
面積が16㎡の場合、一辺の長さは次のように計算します。
一辺 = √16 = 4m
平方根を使うことで、面積から一辺の長さを簡単に求められます。
📏 対角線の長さを調べたいとき
一辺が10cmの正方形のタイルがある場合、対角線の長さは次の通りです。
対角線 = √(10² + 10²)
= √(100 + 100)
= √200 ≈ 14.14cm
こうした計算は、インテリアや工作などで物の大きさを正確に測りたいときに役立ちます。
🏃 地図アプリやゲームの距離計算
スマホの地図アプリやゲームでも平方根が使われます。
例えば、東に3km、北に4km進むと、最短距離は次のように求めます。
最短距離 = √(3² + 4²)
= √(9 + 16)
= √25 = 5km
これは ピタゴラスの定理 に基づく計算です。
🎮 ゲームの攻撃範囲や距離感
ゲームの世界でも、平方根は活躍します。RPGやシューティングゲームでは、キャラクター同士の距離を計算する際に平方根が使われます。攻撃が届くかどうかを判断するための計算が、ゲームの裏で行われています。
🎨 デザインや工作でバランスを取るとき
ポスターや模型を作る際にも平方根は役立ちます。
例えば、面積50cm²の正方形を作りたいとき、一辺は次のように計算します。
一辺 = √50 ≈ 7.07cm
このように平方根を使うと、寸法を正確に決められるため、デザインや工作がより美しく仕上がります。
平方根は「もと」を探す道具 🔎📚💡
このように、平方根は
- 長さを求めるとき
- 揺れや振動を分析するとき
- 美しいデザインを作るとき
など、日常生活のさまざまな場面で使われています。「平方根はただの計算」と思いがちですが、実際には身近なところで役立つ便利な道具です。ある数が「何かを二乗した結果」であるとき、その「もと」を知るために平方根は使われます。
自然界における平方根

実は、自然界には数学的な法則や構造が隠れており、その中に平方根が現れる場面もいくつかあります。以下に代表的な例を詳しく紹介します。
🌻 1. フィボナッチ数列と黄金比、そして平方根
自然界に多く見られる「フィボナッチ数列」(1, 1, 2, 3, 5, 8, 13…)の隣り合う数の比は、だんだんと 黄金比(約1.618) に近づきます。
この黄金比は次の式で表されます:
φ = (1 + √5) / 2
つまり、√5という平方根が、自然の中の美しい比率の中に含まれているのです。以下のような自然物に見られます:
- ヒマワリの種の渦巻き配置
- パイナップルや松ぼっくりの模様
- シダ植物の葉の巻き方(螺旋)
🦴 2. 動物の成長と平方根スケーリング
生物の体の表面積や体積の比率は、平方根や立方根で表されることがあります。
例:動物の代謝量は、体重の 約3/4乗 に比例すると言われています(クレバーの法則)。この考え方の背景には、「体表面積は体積の平方根に近い関係にある」というスケーリング理論があります。
🐌 3. 貝殻や角の成長と平方根
巻貝やヤギの角など、対数螺旋に従って成長する自然物は、成長の過程で √2 や √3 などの比率を含む数学的構造を持っています。
これらの螺旋の角度や大きさの比率は、黄金比とも関係し、結果として 平方根を使った形の変化が現れるのです。
🌱 4. 木の枝分かれや葉の配置
植物が光を効率よく受け取るための配置(「フィロタクシー」と呼ばれます)も、数学的パターンに従っています。
- 137.5度という配置角度(黄金角)
- 葉の位置がフィボナッチ数で決まる
この構造は、(1 + √5)/2 に基づく比率で最も効率的な日照を実現しているという研究もあります。
🌌 5. 惑星の軌道や引力の法則
ニュートンの万有引力の法則において、惑星の速度や周期を表す公式には平方根が出てきます。
- 周期T ∝ √(r³)
- 重力加速度 g = √(F/m)
宇宙の運動も、平方根で成り立っていると言えるほどです。
🧠 6. 生物の感覚のスケール
人間の感覚、たとえば「音の大きさの感じ方(デシベル)」や「明るさの感知」なども、物理量の平方根に比例して感じる傾向があるとされます。
これは「ウェーバー・フェヒナーの法則」に関係しています。
| 自然現象・対象 | 平方根との関係 |
|---|---|
| ヒマワリ、松ぼっくり | 黄金比(√5)による配置 |
| 動物の成長・代謝 | 体表面積と体重の比率が平方根に関係 |
| 貝殻、角 | √2 や √3 に関連する螺旋形の成長 |
| 葉の配置 | フィボナッチ数列 → 黄金比(→ √5) |
| 惑星の運動 | 引力や周期の式に平方根が登場 |
| 人間の感覚 | 感じ方が刺激の平方根に比例(音、光など) |
身近な平方根に関するトリビア

🏠 ①:テレビのインチは平方根で決まる?
テレビやスマホの「インチ数」は、画面の対角線の長さです。縦と横の長さから、三平方の定理(a² + b² = c²)を使って、√(平方根)で対角線を求めることができます。たとえば、縦90cm・横160cmの画面なら、対角線は √(90²+160²) ≈ 183.5cm。これが約72インチに相当します。
📏 ②:タイルの対角線を測るときにも
10cm四方の正方形のタイルの対角線を測りたいとき、√(10²+10²)=√200 ≈ 14.14cm。メジャーでは測りにくい角の長さも、平方根でスムーズに求められます。
🗺️ ③:地図アプリでのルート計算にも使われている
地図アプリやゲームの座標システムでは、2点間の最短距離(直線距離)を計算するときに平方根が使われます。たとえば、ある地点から東へ3km・北へ4km進んだ場合の距離は √(3²+4²)=5km。ピタゴラスの定理そのものですね。
🎮 ④:ゲームの攻撃範囲や判定にも活躍
RPGやシューティングゲームで、相手が「攻撃範囲に入っているかどうか」の計算に使われるのが平方根。プレイヤーと敵の位置をもとに、裏では距離を√で計算しています。
📐 ⑤:正方形の面積から一辺の長さを求める
面積が与えられたとき、一辺を求めるのに使うのが平方根。例:面積が36㎡なら、一辺は √36 = 6m。DIYや部屋のレイアウトでも活用されます。
🎨 ⑥:黄金比の中に登場
黄金比は (1 + √5)/2 ≈ 1.618… という式で表され、建築や美術で「最も美しい比率」とされています。つまり、美の根本に平方根が隠れているのです。
🏢 ⑦:地震に強い建物設計にも関係
建物の固有周期(揺れやすさ)は、T = C × √H(Hは高さ)で近似されることがあります。つまり、建物がどのくらい揺れるかを予測するのに平方根が必要です。
📊 ⑧:統計の「標準偏差」は平方根から
ばらつきの指標である標準偏差は「分散の平方根」で求めます。つまり、データの広がりを見るために、私たちは無意識に平方根を使っているのです。
📚 ⑨:円の面積から半径を求められる
円の面積 S = πr² の逆を使って、r = √(S/π) で半径を求めることができます。庭に円形のスペースを作るときなど、実用性の高い計算です。
🧮 ⑩:√の記号は500年前から存在
「√」という記号は、16世紀にドイツの数学者ルドルフが使ったのが始まりとされます。元々は「根(radix)」の頭文字「r」に由来すると言われています。
🧠 ⑪:√2 の発見は古代ギリシャでの大事件
√2 は分数で表せない「無理数」の最初の発見とされています。これはピタゴラス学派の信念をくつがえすほどの大問題でした。発見者が処罰されたという伝説もあるほどです。
📏 ⑫:「完全平方数」だけが平方根を持つわけではない
√9 = 3 のように整数の平方根を持つ数を「完全平方数」と言いますが、他の数(例:√7)は無理数です。それでも実数として計算できるのが現代数学の強みです。
🔬 ⑬:物理の公式にもたくさん出てくる
自由落下、エネルギー、速度、光、音の伝播など、平方根は多くの物理公式の中核に登場します。例えば、落下距離 s = ½gt² → t = √(2s/g)。
📐 ⑭:設計や建築のバランスを整えるためにも使われる
家具の配置や庭の設計などでも、エリア(面積)を指定して正方形や長方形の辺を求めるときに平方根が便利です。目に見える「バランス」は計算から生まれます。
🧩 ⑮:IQテストやパズルでも活躍
「√49はいくつ?」といった問題はもちろん、「2点間の最短距離は?」といった図形問題でも平方根の知識が問われます。論理思考の力試しにも登場します。
レオナルド・ダ・ヴィンチと平方根
レオナルド・ダ・ヴィンチと平方根には、数学と芸術が融合した興味深い関係があります。
🎨 1. ダ・ヴィンチは黄金比(φ)に強い関心を持っていた
黄金比は数学的に以下の式で表されます:
φ(ファイ)= (1 + √5) / 2 ≈ 1.618…
この式に 平方根(√5) が含まれている点が重要です。黄金比は美しいプロポーションを示す比率として知られており、ダ・ヴィンチはこの比率を多くの芸術作品や図面に取り入れていました。
📐 2. 『ウィトルウィウス的人体図』と数学的比率
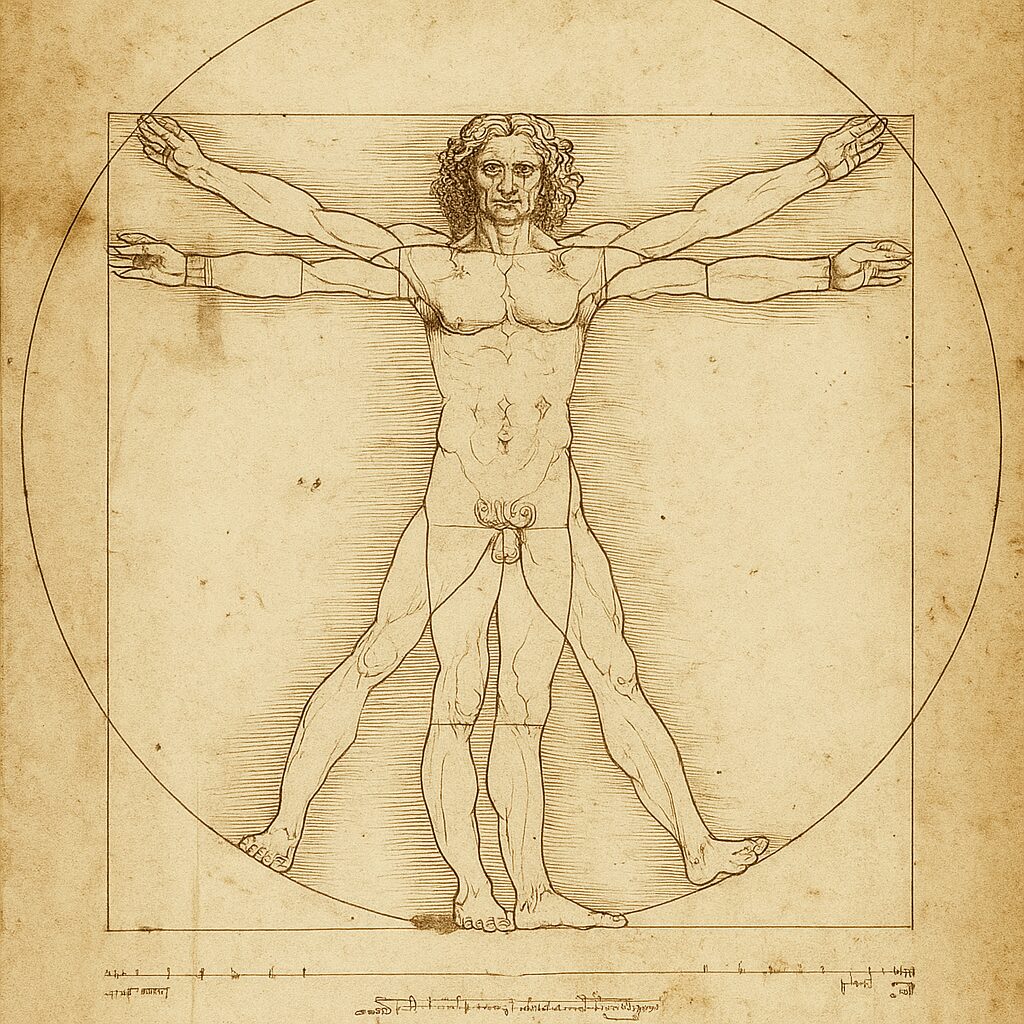
ダ・ヴィンチの代表作の一つ『ウィトルウィウス的人体図』では、人体を円と正方形にぴったりと収める図を描いています。この作品は、人体が数学的比率に基づいて構成されているという古代ローマの建築家ヴィトルウィウスの理論を視覚化したものです。
- 腕を広げた長さ ≈ 身長
- へそを中心とした円の半径 ≈ 身長の半分
こうした長さや比率の計算の背景には、平方根が関係する幾何学的な関係が使われています。
📊 3. ダ・ヴィンチはユークリッド幾何学と代数学を応用
ダ・ヴィンチは単なる画家ではなく、科学者・数学者でもありました。彼はユークリッドの『原論』を研究し、図形の面積や長さの関係、そしてそれを計算する方法として平方根を含む操作を自らのスケッチブックやノートで何度も試みています。
🧮 4. 立体図形の研究と平方根
『レオナルド・ダ・ヴィンチの多面体図』と呼ばれる作品群では、正多面体やその変形を美しく描いています。これらの立体を描くには、辺の長さや角度、面の比率などを正確に計算する必要があり、斜辺や対角線を求めるための平方根が欠かせません。
📚 5. レオナルドとルカ・パチョーリの共著:『神聖比例論』
ダ・ヴィンチは、数学者ルカ・パチョーリの著書『神聖比例論(De Divina Proportione)』の図版を描いたことでも知られています。この本は、黄金比の数学的性質と美術・建築への応用を詳しく解説したもので、黄金比を含む図形には常に**√5 が計算に現れます**。
🔍 まとめ:ダ・ヴィンチにとって平方根とは?
- 単なる数式ではなく、「自然と美の調和を説明する道具」でした。
- 建築・人体・絵画・幾何学のどれをとっても、彼の探究には平方根が密接に関係しています。
- 数学の美しさを芸術に表現した人物として、ダ・ヴィンチはまさに「ルネサンスの平方根マスター」と言えるかもしれません。
まとめ
平方根は、一見すると数学の授業でしか使わないような難しいものに見えるかもしれません。でも、実は私たちの身の回りにある様々な現象や製品、デザインの中にひっそりと隠れていて、その「もと」を知るための大切な役割を果たしているんです。
今回紹介した平方根の身近な例以外にも、平方根が使われている場面はたくさんあります。ぜひ、日常生活の中で「これって、もしかして平方根が関係してる?」と考えてみてください。きっと、数学がもっと面白く感じられるはずですよ!









